Les nombres complexes

 

Exercices

 

Rappels

plan d'Argand Cauchy

z = x + iy

z est l'affixe de M.

θ = ( Or,) à 2 π près
r = OM

L'argument défini à 2 π près de z est θ tel que z = r (cos θ + i sin θ).

Le module représente une distance |z| = OM, si A est d'affixe z_A et B z_B alors
AB = |z_B z_A|

 

Proprietés

Pour tout z et z' complexes

|zz'| = |z| |z'|

|1/z| = 1/|z|

|z ²| = |z|²

|z/z'| = |z|/|z'|

|z + z'| <ou = |z| + |z'|

Arg (1/z) = - Arg z (2π)

Arg (z^M) = M Arg z (2π) pour tout M appartenant à Z

Arg (zz') = Arg z + Arg z' (2π)

Arg (z'/z) = Arg z - Arg z' (2π)

 

Formules d'Euler et Moivre

Moivre : (cos θ + i sin θ )ⁿ = cos nθ + i sin θ

e^i(θ+θ') = e^iθ - e^iθ'

Donc cos θ = 1/2 ( e^iθ + e^-iθ)
sin θ = 1/2i ( e^iθ - e^-iθ)

 

Racines carrées d'un nombre complexe

 

Exemple : Résoudre z² = 1 + i, c'est chercher les racines carrés de 1 + i

Posons z = x+ iy

z² = 1 + i
(x+iy)² = 1 + i
x² - y² + 2 ixy = 1 + i

x² - y ² = 1 (1)
2 xy = 1 (2)

On a l'égalité des modules
|z²| = |1 + i|
x² + y² = √2 (3)

(1) + (3) : x² = (1 + √2) / 2
(3) - (1) : y² = (√2 - 1) / 2

Comme xy est positif, x et y sont du même signe.

x₀ = √((1 + √2) / 2)
y₀ =√( (√2 - 1) / 2)
ou -x_o et -y_o

Les solutions sont z₀= x₀ + iy₀, z = - z₀

On pose z = r e^iθ

1 + i = r e^iθ

z² = 1 +i si et seulement si r² e^2iθ = √2 e^iπ/4

r² = √2
2θ = π/4 + 2 kπ, k appartenant à Z

r = 2^1/4
θ = π/8 + k π

Les 2 solutions sont z₀ = 2^1/4e^iπ/8 et z₁ = 2^1/4e^i(π/8+π) = - z₀ .

 

Les racines n^ième d'un nombre complexe sont les solutions de l'équation zⁿ = z. Si z=1 ce sont les racines n^ième de l'unité.

zⁿ =1
z = r e^iθ
zⁿ = rⁿ e^inθ

On identifie

rⁿ = 1
nθ = 2 kπ

r = 1 car n supérieur ou égal à 0.
θ = 2 kπ / n

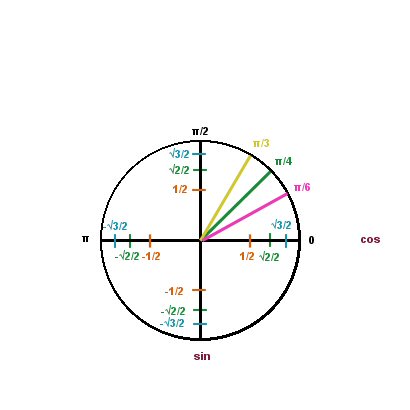
Cercle trigonométrique